1.3.8 Ángulo Completo

1.3.8 Ángulo Completo
es un angulo que mide 360 (grados) por el cual son lines o vertices que se encuentran de lado a ladoes un angulo que mide 360 (grados) por el cual son lines o vertices que se encuentran de lado a lado.

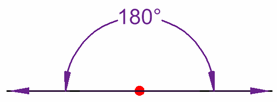
1.3.7 Ángulo Llano

1.3.7 Ángulo Llano
Un ángulo llano cambia la dirección para apuntar en la dirección contraria, se ve como una línea recta.
Su medida es de 180° (media revolución, o dos ángulos rectos).Un ángulo llano cambia de dirección para apuntar en la contraria.

1.3.6 Ángulo Concavo

1.3.6 Ángulo Concavo
El ángulo cóncavo mide más de 180º y menos de 360º.

1.3.5 Ángulo Convexo

1.3.5 Ángulo Convexo
Ángulo convexo es el conjunto de puntos comunes a dos semiplanos de un mismo plano, cuyos contornos tienen un punto común, denominado vértice del ángulo.

Para ello, se delimitan las rectas convergentes que conforman el ángulo por dos semirrectas con vértice el punto común. Así, los puntos del ángulo convexo serían aquellos que no perteneciendo a las semirrectas, o lados del ángulo, quedan comprendidos entre las mismas, es decir, son puntos interiores del mismo ángulo.

Por regla general, siempre que se hace mención del término ángulo se hará referencia al ángulo convexo.

1.3.4 Ángulo Obtuso

1.3.4 Ángulo Obtuso
Un ángulo obtuso es aquel que es superior a 90º e inferior a 180º, esto es, entre y Rad.)

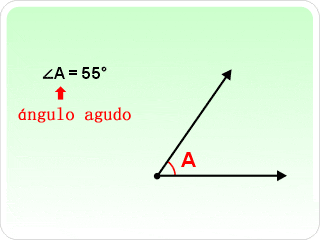
1.3.3 Ángulo Agudo

1.3.3 Ángulo Agudo
Es el ángulo formado por dos semirrectas con amplitud mayor de 0º y menor de 90º. A la unión se le llamo vértice punto de inicio o de encuentro.

1.3.2 Ángulo Recto

1.3.2 Ángulo Recto
Ángulo que mide 90° o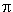 /2 radianes. Es el ángulo entre dos líneas perpendiculares, como la arista de un cuadrado, o dos planos perpendiculares, como la pared y el piso.

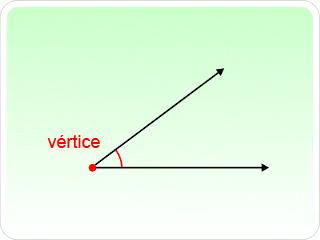
1.3.1 Ángulos

1.3.1 Ángulos
Figura formada por dos semirrectas que parten del mismo punto inicial. A las dos rectas se les denomina lados del ángulo y al punto inicial se le llama vértice del ángulo. 

1.2.5 Planos

1.2.5 Planos
Suele representarse el plano como una figura delimitada por bordes irregulares (no es apropiado usar bordes regulares porque no es una figura finita, y puede prestarse a confusión), y puede notarse con una letra del alfabeto griego. Es bidimensional.

1.2.4 Segmento de Recta

1.2.4 Segmento de Recta
si tomamos 2 puntos en una recta (T y S), el segmento de recta sera el conjunto de puntos comprendidos entre T y S

se caracteriza por que :
Es una porcion o parte de una recta. es la menor distancia posible entre dos puntos. y por que tiene un principio y un final, por ende es suceptible de ser medido.

1.2.3 Semirrecta

1.2.3 Semirrecta

Una SEMIRRECTA  es  una secuencia  de  puntos  que  se  prolonga en  un  solo  sentido y  tiene  un  punto de  origen.En este  caso se  llama  A. Pero no  tiene punto final.

1.2.2 La Recta

1.2.2 La Recta
Se designan mediante dos de sus puntos o mediante una letra minúscula.Dos puntos determinan una recta.Una recta indica una dirección y dos sentidos contrarios, según se recorra la recta de izquierda a derecha o de derecha izquierda.

1.2.1 El Punto

1.2.1 El Punto
Los puntos no tienen dimensiones.Por tanto carecen de longitud, anchura y altura.Un punto indica una posición. en el plano o en el espacio.Los puntos se nombran con letras mayúsculas.

1.1 Sobre La Geometria

1.1.1 Historia de la Geometria

La geometría, es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras en el plano o el espacio, incluyendo: puntos, rectas, planos, politopos (que incluyen paralelas, perpendiculares, curvas, superficies, polígonos, poliedros, etc.). Es la base teórica de la geometría descriptiva o deldibujo técnico. También da fundamento a instrumentos como el compás, el teodolito, el pantógrafo o el sistema de posicionamiento global. Sus orígenes se remontan a la solución de problemas concretos relativos a medidas. Tiene su aplicación práctica en física aplicada, mecánica, arquitectura, cartografía, astronomía, náutica, topografía, balística, etc. Y es útil en la preparación de diseños e incluso en la elaboración de artesanía.








1.1.2 Matematicos y Filosofos

Pitágoras (c. 582-c. 500 a.C.), filósofo y matemático griego, cuyas doctrinas influyeron mucho en Platón. Nacido en la isla de Samos, Pitágoras fue instruido en las enseñanzas de los primeros filósofos jonios Tales de Mileto, Anaximandro y Anaxímenes. Se dice que Pitágoras había sido condenado a exiliarse de Samos por su aversión a la tiranía de Polícrates. Hacia el 530 a.C. se instaló en Crotona, una colonia griega al sur de Italia, donde fundó un movimiento con propósitos religiosos, políticos y filosóficos, conocido como pitagorismo. La filosofía de Pitágoras se conoce sólo a través de la obra de sus discípulos. ver mas sobre pitagoras.






1.1.3 Conceptos Basicos

Conceptos básicos de geometría

La geometría trata de la medición y de las propiedades de puntos, líneas, ángulos, planos y sólidos, así como de las relaciones que guardan entre sí. A continuación veremos algunos conceptos relacionados con la geometría.

Punto: Es la representación de una posición fija del espacio. No es un objeto físico, por lo tanto carece de forma y dimensiones.

ínea: Es una sucesión infinita de puntos.

Las líneas se clasifican basicamente en:

recta,

poligonal

curva

Recta’‘’: Línea de dirección constante. Una recta puede ser definida por dos puntos a los que une recorriendo su menor distancia.

Partes de una Recta:

•semirrecta: cada una de las dos partes en que divide a una recta uno cualquiera de sus puntos

•segmento: porción de una recta comprendida entre dos de sus puntos.

Posición Relativa entre dos Rectas

Según la posición relativa en que se encuentren dos rectas, se definen como:

•rectas que se cortan: si tienen un punto en común. En este caso están contenidas en un plano

•rectas paralelas: si mantienen indefinidamente la distancia entre ellas. En este caso están contenidas en un plano

•rectas que se cruzan: si no se cortan ni son paralelas. En este caso no están contenidas en un plano

Poligonal’‘’:Línea formada por segmento rectos consecutivos no alineados. Se clasifican en:

•poligonal abierta: si el primer y último segmentos no están unidos

•poligonal cerrada: si cada segmento esta unido a otros dos.

‘Ángulo’‘’: Porción de un plano comprendida entre dos semirrectas de origen común